Machine learning (ML) has been successfully integrated into modern Cyber-Physical Systems (CPS), demonstrating remarkable progress in addressing sequential and complex decision-making challenges across various domains, including autonomous driving, chemical process optimization, and robot locomotion. These learning-enabled systems hold immense potential to revolutionize industrial processes, leading to substantial economic benefits.

However, real-world incidents highlight significant challenges in ensuring the safety of ML-based techniques. The AI Incident Database (AID) reveals that, despite achieving impressive performance, ML systems often lack formal safety guarantees. For example, the National Highway Traffic Safety Administration (NHTSA) reported 351 car crashes involving advanced driver assistance systems in the United States between July 2023 and March 2024.

These findings underscore the urgent need for learning-enabled systems that deliver not only high performance but also verifiable safety, addressing the increasing market demand for reliable and safe ML solutions. To overcome these limitations, we explore the integration of machine learning methods with physics-model-based design. By leveraging physics-based models, we aim to enhance safety assurance, improve sampling efficiency, and promote the generalizability of learning-based decision-making systems.

Physics-model-regulated Deep Reinforcement Learning Architecture (Phy-DRL)

Deep reinforcement learning (DRL) synthesizes control policies by interacting with the environment, effectively addressing non-linearity and uncertainties in complex control tasks while achieving impressive performance. However, applying DRL to safety-critical autonomous systems remains a significant challenge. A key issue lies in the control policies parameterized by deep neural networks (DNNs), whose behaviors are difficult to predict and verify, raising concerns about safety and stability.

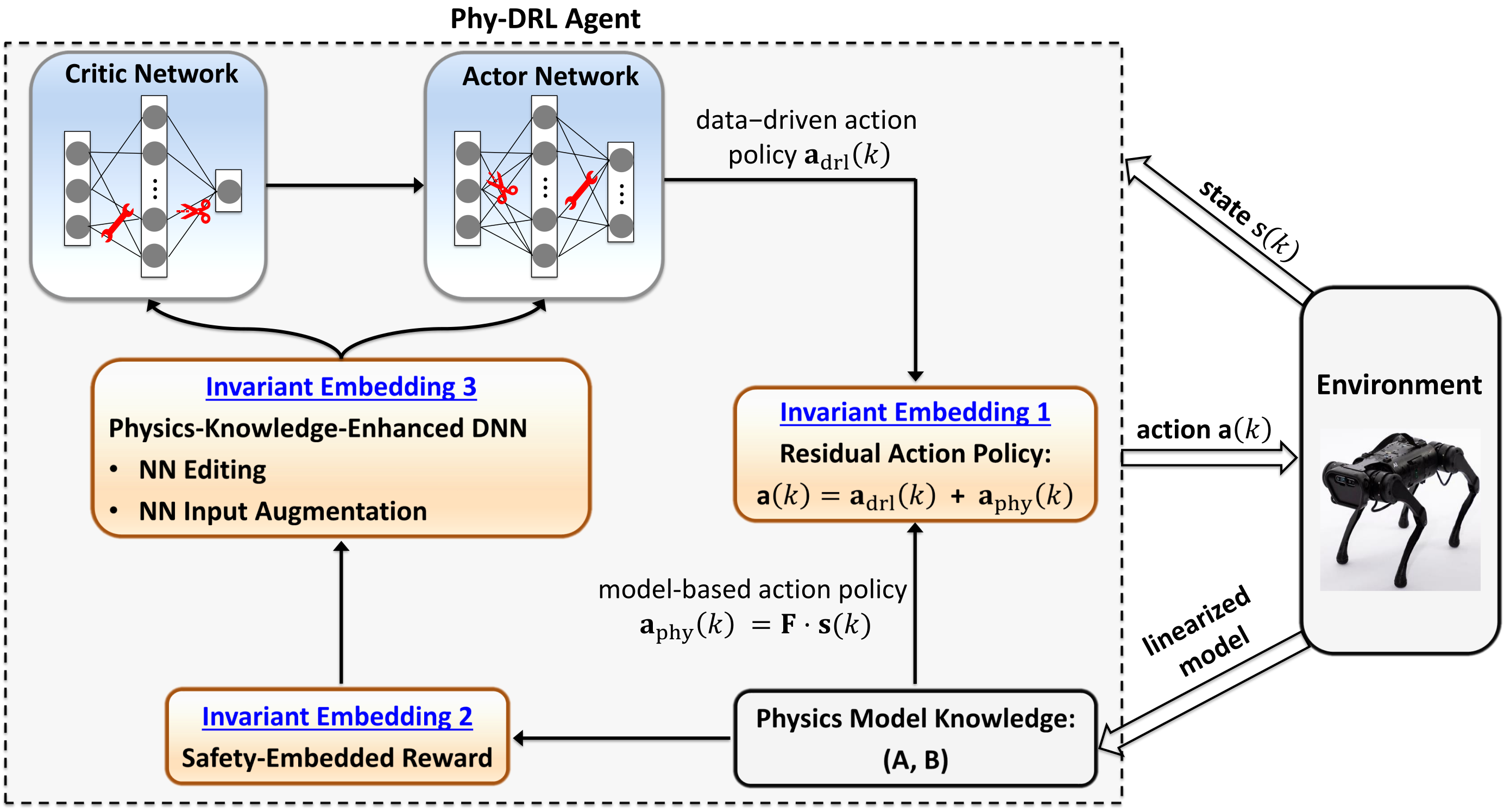
In many practical autonomous systems, approximations of nonlinear system dynamics can be obtained through reasonable linearization. These approximations allow for the design of model-based controllers with verifiable properties for system control. Inspired by the residual control framework, we propose a novel physics-model-regulated DRL framework that integrates model-based knowledge to guide and regulate the purely data-driven DRL approach, as illustrated in the figure.

Specifically, we incorporate Lyapunov stability theory with the linearized model to design a Lyapunov-like reward function. This encourages the DRL agent to learn policies that stabilize the system and maintain operation within the safety envelope. Additionally, we mathematically derive safety and stability testing conditions using model knowledge to ensure guaranteed safety. Finally, we integrate the model-based controller with the DRL under the residual control framework to produce robust and reliable control commands.

Physics-model-guided Worst Case Sampling

Real-world accidents in learning-enabled CPS frequently occur in challenging corner cases. During the training of deep reinforcement learning (DRL) policy, the standard setup for training conditions is either fixed at a single initial condition or uniformly sampled from the admissible state space. This setup often overlooks the challenging but safety-critical corner cases. From a control-theoretic perspective, system-state samples close to the safety boundary represent the corner cases where a slight disturbance or fault can take a system out of control. Intuitively, focusing the training on such corner-case samples will enable a more robust and safe action policy. In the safe DRL community, how to define those corner cases and how to use them for learning safe policies remains unclear.

To bridge the gap of training on corner cases in the existing literature, we propose a formal definition of the worst case for DRL based on the system's dynamics model. Furthermore, we propose an algorithm to efficiently generate the worst cases for policy learning. At last, we integrate the worst-case sampling into the Phy-DRL framework to learn safer and more robust policies. The integrated Phy-DRL framework defines worst-case samples as the state of the system located on the boundary of a safety envelope. These corner-case samples are not often visited during training via random sampling. Worst-case sampling thus lets Phy-DRL's training focus on the safety boundary, enabling a more robust and safe action policy.

We demonstrate the worst-case empowered Phy-DRL in three case studies, including a cart-pole system, a 2D quadrotor, and a quadruped robot, showing remarkable improvement in sampling efficiency and safety assurance.

Safe Runtime Learning

Real-world applications often expose modern Cyber-Physical Systems (CPS) to unprecedented environmental changes, leading to out-of-distribution (OOD) samples that can cause failures in pre-trained policies. To ensure the pre-trained policy remains safe and optimal under new operational conditions, it should adapt safely and efficiently at runtime. To achieve this, we propose a runtime learning architecture based on the Simplex framework.

The proposed architecture has three interactive components: a high-performance (HP)-Student, a high-assurance (HA)-Teacher, and a Coordinator. The HP-Student is a high-performance but not fully verified Phy-DRL (physics-regulated deep reinforcement learning) agent that performs safe runtime learning in real plants, using real-time sensor data from real-time physical environments. On the other hand, HA-Teacher is a verified but simplified design that focuses on safety-critical functions. As a complementary, HA-Teacher's novelty lies in real-time patch for two missions: i) correcting unsafe learning of HP-Student, and ii) backing up safety. The Coordinator manages the interaction between HP-Student and HA-Teacher. Powered by the three interactive components, the runtime learning machine notably features i) assuring lifetime safety (i.e., safety guarantee in any runtime learning stage), ii) tolerating unknown unknowns, iii) addressing Sim2Real gap, and iv) automatic hierarchy learning (i.e., safety-first learning, and then high-performance learning). Experiments involving a cart-pole system, two quadruped robots, and a 2D quadrotor, as well as comparisons with state-of-the-art safe DRL, fault-tolerant DRL, and approaches for addressing Sim2Real gap, demonstrate the machine's effectiveness and unique features.